Your Attention Please: Understanding AI Attention -- Pure AI

Your Attention Please: Understanding AI Attention

By Pure AI Editors
07/01/2025

The key component of large language models (LLMs) such as GPT-x, is a software module called a Transformer. The key component of a Transformer is called an Attention module.

Suppose an input sequence is the sentence, "Watch the man code." Briefly and loosely speaking, the Attention mechanism computes a vector of values for each of the four words in the input, where the values represent the words with contextual information that can be used to determine the strength of the relationship, or relevance, between the words. In this example, the word "the" is most closely associated to the word "man", so the attention values for "the" and "man" can be used to compute a measure of their strong association.

Why Yet Another Article on AI Attention?
It's not necessary to have a full understanding of Attention in order to use LLM applications such as ChatGPT. But having a basic grasp of Attention is useful to understand how LLM applications work, their strengths and weaknesses, and help you decipher marketing noise from companies that are trying to sell LLM related services to you.

There are many dozens of online articles that explain the Attention mechanism. These explanations of Attention tend to be either 1.) at a very low level, dissecting the underlying code in great detail, or 2.) at a very high level, ignoring all the complex details. Low-level explanations of Attention are only useful for software engineers with advanced coding skills. High-level blah-blah-blah explanations don't provide any meaningful information.

This article explains Attention at an intermediate level -- low enough to provide useful information, but not so low as to overwhelm you with complex engineering details. This article is based on training materials provided to employees at a huge technical company located in Redmond, Washington.

How Attention is Related to Embedding and Positional Encoding
One of the reasons why the Attention mechanism is difficult to understand is that it's part of a larger LLM process. This overall process is illustrated in Figure 1. Suppose an input sentence is, "Watch the man code." The first step is to break the sentence down into separate words (technically, tokens). This process is called tokenization.

Figure 1: How Attention Is Related to Embedding and Positional Encoding — **[Click on image for larger view.]** *Figure 1:* How Attention Is Related to Embedding and Positional Encoding

The next step is to convert the words/tokens into numeric vectors. For example, the word "watch" might be converted into [0.36, 1.67, . . 0.92]. This process is called word embedding. The idea is that an English word can have multiple meanings. For example, "watch" can mean the act of observing something, or a device for telling time.

After embedding, the numeric vectors representing the words are augmented with values that indicate their position within the input sentence. This process is called positional encoding. The idea is that position is important. For example, "watch the man code" has a different meaning than "code the man watch."

After positional encoding, the numeric vectors representing the words and their position within the input sentence are sent to the Attention mechanism where there are converted into more complex vectors that have relevance information added. The idea is subtle. The relevance information encapsulates how the words are related to each other. For example, in "watch the man code," the word "the" is closely associated with the word "man."

The final result of the embedding, positional encoding, and attention process is a set of vector values that accurately describe the source input sentence.

Essential Preliminaries
The Attention mechanism is complicated in part because it uses five math ideas that most non-engineers are not familiar with. Specifically, Attention uses vectors (aka tensors), matrices, matrix multiplication, matrix transpose, and softmax scaling. Fortunately, these five concepts are easily explained.

A vector is an array of numbers such as [0.37, -1.93, 0.22]. A tensor is essentially a vector that can be processed by very fast GPU processors.
A 2D matrix is a rectangular grid of numbers. For example, a 3-by-4 (3 rows, 4 columns) matrix looks like
```
     0.12  0.98 -1.05  2.27
     1.14 -0.37  0.52  0.92
     0.67  1.73  0.51 -0.44
```
A 2D matrix can be interpreted as a set of row vectors stacked on top of each other.
It is possible to multiply two matrices together. If matrix A has shape m-by-n and matix B has shape n-by-p, the A * B has shape m-by-p. For example, a 3-by-5 matrix times a 5-by-2 matrix has shape 3-by-2.

A matrix transpose swaps the rows with the columns. For example, if a 3-by-4 matrix is:

     0.12  0.98 -1.05  2.27
     1.14 -0.37  0.52  0.92
     0.67  1.73  0.51 -0.44

then the transpose is the 4-by-3 matrix:

      0.12  1.14  0.67
      0.98 -0.37  1.73
     -1.05  0.52  0.51
      2.27  0.92 -0.44

The softmax function scales the elements in a vector so that they sum to 1. For example, softmax([3.0, 5.0, 2.0]) is [0.12, 0.84, 0.04]. The softmax calculations are a bit tricky, but understanding those calculations isn't needed to understand Attention.

The Attention Mechanism
The Attention mechanism is illustrated in Figure 2. The input to Attention is a matrix that represents words in a sentence. If there are four words in the input, and the embedding dimension is set to 3, then the input has shape 4-by-3. In practice, the embedding dimension is usually about 100.

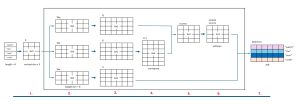Figure 2: The Attention Mechanism — **[Click on image for larger view.]** *Figure 2:* The Attention Mechanism

The first step in Attention is to create three weight matrices, usually referred to as Wq, Wk, Wv. The q, k, and v stand for "queries", "keys", "values" but these three terms have no obvious interpretation. Initially, the values in the weights matrices are small random numbers. Their actual values are determined during the LLM training process.

The three weight matrices will all have the same number of rows as the embedding dimension. The number of columns in the weight matrices is somewhat arbitrary and must be determined by trial and error. The number of columns is sometimes called the hidden dimension or the weights dimension. At the time this article was written, the Wikipedia entry on Attention calls the weights dimension "number of neurons", which is not meaningful.

If the input has four words, and the embedding dimension is set to 3, and the weights dimension is set to 6, the three weights matrices, Wq, Wk, Wv, will have shape 3-by-6.

Next, three matrices called Q, K, V are computed using matrix multiplication. If the input matrix is called X, then Q = X * Wq, K = X * Wk, V = X * Wv. If X is 4-by-3, and the W matrices are 3-by-6, then Q, K, V all have shape 4-by-6. This process has no obvious interpretation, and it's best not to overthink it.

The K matrix is used to compute a K.T matrix which is the transpose of K. If K has shape 4-by-6, then K.T has shape 6-by-4. Again, this step has no obvious reason other than "it works."

Next, a scores matrix is computed as Q * K.T. If Q has shape 4-by-6, and K.T has shape 6-by-4, the scores matrix has shape 4-by-4. In general, if the input sequence has n words, the scores matrix has shape n-by-n. Once again, it's best not to overthink the meaning of the scores matrix.

Next, a scaled scores matrix is computed by applying the softmax function to each of the rows of the scores matrix. In code: softmax(scores / np.sqrt(wts_dim), axis=1). This means takes the scores matrix, divide each value by the square root of the weights dimension (to keep the values smaller), then apply softmax on the rows (axis=1) so that the values in each row sum to 1. As before, there's no obvious interpretation of this step, so don't overthink. If the scores matrix has shape 4-by-4 then the scaled scores matrix has the same shape.

The last step in Attention is to multiply the scaled scores matrix by the V matrix. If the scaled scores matrix has shape 4-by-4 (number words by number words) and the V matrix has shape 4-by-6 (number words by weights dimension), then the final Attention matrix has shape 4-by-6 (number words by weights dimension).

To recap, for an input sentence with n words and a specified embedding dimension (often 100 in practice), word embedding and positional encoding produce an n-by-embed_dim input matrix that encapsulates the word meanings and word positions. Attention requires a weights dimension (determined by trial and error but often about the same as the embedding dimension).

The LLM training process computes values for the internal Wq, Wk, Wv weights matrices, and after the result of non-obvious but deterministic matrix multiplications, transpose, and softmax scaling operations, an Attention matrix with shape n-by-weights_dim that encapsulates word meanings, word positions, and word relevance is generated. Whew!

There are several different types of AI Attention. This article explains the most basic form, called self-attention, because it relates the words in a input sentence to themselves. A form called cross-attention relates input words to output words, for example in an LLM question-answer system.

Wrapping Up
The Pure AI editors asked Dr. James McCaffrey to comment. McCaffrey directs the data science and research efforts at Nukleus, a data analytics company located near Redmond, Washington. Before Nukleus, McCaffrey worked at Microsoft where he developed most of the content ideas presented in this article.

"The Attention mechanism is arguably one of the most important algorithms in the history of computer science, and having a basic understanding of Attention is usually essential for most people working with AI large language models," he said.

"We tried to use existing online content to explain the AI Attention mechanism to a broad audience of business and technical people, but that content just didn't work well. The content presented in this article has successfully gotten hundreds of people started with AI Attention."