How-To
Researchers Explore Machine Learning Hyperparameter Tuning Using Evolutionary Optimization
Efficient tuning techniques for large machine learning models can produce significant time and cost savings.
- By Pure AI Editors
- 11/01/2022
Researchers at Microsoft have demonstrated that an old technique called evolutionary optimization is effective for tuning complex machine learning models with billions of parameters and configuration settings. Tuning the hyperparameters of a large machine learning model can cost hundreds of thousands of dollars of compute time, so efficient tuning techniques can produce significant time and cost savings.
The Problem
When data scientists create a machine learning prediction model, there are typically about 10 to 20 hyperparameters -- variables where the values must be determined by trial and error guided by experience and intuition. There are two types of model hyperparameters: architecture and training. Architecture hyperparameters specify the design of a model. Examples include the number of hidden layers, the number of hidden nodes in each hidden layer, choice of activation functions (tanh, relu and so on) and choice of weight initialization algorithm (uniform, xavier and so on). Training hyperparameters specify how to train a model. Examples include learning rate, batch size and dropout rate.
Finding good values for model hyperparameters is called hyperparameter tuning. For simple machine learning models, the most common tuning approach used by data scientists is to manually try different permutations of hyperparameter values. The manual tuning process is subjective and so no two data scientists would explore the same sets of hyperparameter values.
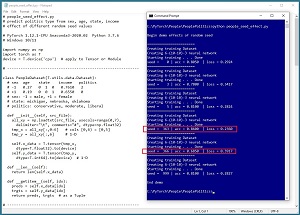 [Click on image for larger view.] Figure 1: Different Seed Hyperparameter Values Have a Big Impact on Model Accuracy
[Click on image for larger view.] Figure 1: Different Seed Hyperparameter Values Have a Big Impact on Model Accuracy
Different sets of hyperparameter values can have a big impact on model effectiveness. The screenshot in Figure 1 shows an example of varying the seed value used for random number generation. The program seed value is a combined architecture and training hyperparameter because the value controls the weight initialization architecture hyperparameters, and also the order in which training data items are processed.
The demo program creates a model that predicts a person's political leaning (conservative, moderate, liberal) based on sex, age, state of residence and income. Using six different seed values of [0, 3, 5, 363, 366, 999], the associated six models ranged from a weak 68.5 percent accuracy to a strong 86 percent accuracy.
Random Search and Grid Search
In production scenarios, hyperparameter tuning is performed programmatically rather than manually. The two most common programmatic tuning techniques are random search and grid search. In random search, a range of possible values is specified for each hyperparameter. For example, the range of possible values for a learning rate hyperparameter might be something like [0.0001, 0.0500]. The tuning program selects a random value for each hyperparameter, then creates, trains, and evaluates a model using the set of hyperparameter values.
In grid search, instead of specifying a range of values for each hyperparameter, a set of discrete values is specified. For example, a learning rate set might be [0.0001, 0.0010, 0.0050, 0.0080, 0.0100]. The tuning program selects and uses a random value for each hyperparameter.
Random search is simple but often wastes too much time exploring poor sets of hyperparameter values. Grid search is somewhat more principled, but it's usually not possible to investigate all possible permutations of hyperparameter values. For example, suppose a model under development has 10 hyperparameters and each hyperparameter can be one of just eight possible values. There are 8 * 8 * . . * 8 = 8^10 = 1,073,741,824 possible permutations of hyperparameter values to evaluate.
Evolutionary Optimization
An evolutionary optimization algorithm is loosely based on the biological mechanisms of crossover and mutation. A population of possible solutions is maintained. A new child solution is generated by combining a good parent solution with another parent solution, and then the child is mutated slightly. Expressed in high-level pseudo-code:
create population of random solutions
loop max_generation times
pick two parent solutions
use crossover to create a child solution
use mutation to modify child solution
evaluate the child solution
replace a weak solution in population with child
end-loop
return best solution found
The diagram in Figure 2 illustrates crossover and mutation. The diagram corresponds to a hyperparameter tuning problem where there are 10 hyperparameters and each hyperparameter can be one of eight possible index values (0 to 7) that reference an array of specific hyperparameter values.
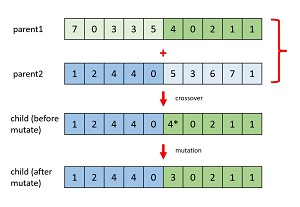 [Click on image for larger view.] Figure 2: Evolutionary Optimization Operations
[Click on image for larger view.] Figure 2: Evolutionary Optimization Operations
Evolutionary optimization is a metaheuristic, meaning it's a set of general guidelines rather than a rigid set of rules. There are many possible implementations for each operation. For example, the crossover point can be fixed at the middle of each child, or the crossover point can vary randomly. For mutation, a new mutate value can vary by 1 from the current value (increase or decrease), or a new mutate value can be any value.
Hyperparameter Tuning Using Evolutionary Optimization
The screenshot in Figure 3 illustrates an example of hyperparameter tuning using evolutionary optimization. The demo corresponds to a scenario where there are 10 hyperparameters and each hyperparameter value ranges from 0 to 7. The demo is configured so that the optimal solution is [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] and the error for any solution is the sum of the index values in the solution.
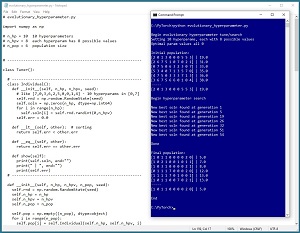 [Click on image for larger view.] Figure 3: Demo of Hyperparameter Tuning Using Evolutionary Optimization
[Click on image for larger view.] Figure 3: Demo of Hyperparameter Tuning Using Evolutionary Optimization
The demo sets up an initial population of six random possible solutions. Of these six, the best set of hyperparameters is [2, 0, 1, 3, 0, 0, 0, 5, 5, 3] with model error of 19.0. The demo iterates through just 60 generations of children, which is just a tiny fraction of the over one billion possible permutations. The demo finds a very good solution of [1, 0, 1, 1, 0, 0, 0, 0, 2, 0]. In a non-demo scenario, each possible solution in the population would run in parallel on separate machines.
Distributed Grid Descent
A specialized form of evolutionary optimization for hyperparameter tuning is described in the 2020 research paper "Working Memory Graphs" by R. Loynd et al. The technique is called Distributed Grid Descent (DGD) to distinguish it from other techniques.
The DGD hyperparameter tuning algorithm uses mutation but does not use crossover. DGD sets up an initial population of 100 possible sets of hyperparameter solutions. The DGD algorithm evaluates candidate solutions on separate machines and updates best results as evaluations are completed.
Everything Old Is New Again
The Pure AI editors spoke with Dr. James McCaffrey from Microsoft Research, who commented, "Evolutionary optimization for hyperparameter tuning was used as early as the 1980s when even simple neural prediction models were major challenges because of the limited machine memory and CPU power."
He added, "The recent focus on huge prediction models for natural language processing based on transformer architecture, where a single training run can take days and cost thousands of dollars, has spurred renewed interest in evolutionary optimization for hyperparameter tuning. Our explorations indicate that evolutionary optimization is well-suited for the new generation of complex machine learning models with billions of permutations of hyperparameter values.
"In production scenarios, there are two types of prediction problems. Small machine learning models, consisting of up to about 1 million parameters, can be tackled by most companies, even those with limited budgets. Large models require significant resources and can be tackled only by companies with large budgets. Evolutionary optimization for hyperparameter tuning is a technique that can be used by even small companies."