How-To
Homomorphic Encryption Makes Slow But Steady Progress
Homomorphic encryption allows computation directly on encrypted data, an approach that has so far been plagued by poor peformance compared to operations on unencrypted data. But it's getting there, Pure AI editors explain.
- By Pure AI Editors
- 07/16/2020
Homomorphic encryption is a special type of data encryption that allows computation directly on the encrypted data. So, why is this important? Consider the scenario shown in Figure 1. Imagine you have some data that contains ultra-sensitive information such as hospital patients' medical records, customer credit card numbers, or military application data.
You want to use your data to create a powerful machine learning system, but your organization doesn't have the technology infrastructure to do so locally. Therefore, you want to process your data using a sophisticated cloud system.
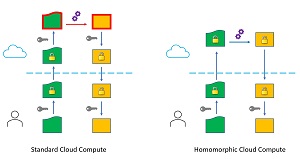 [Click on image for larger view.] Figure 1: Standard Cloud Compute and Homomorphic Cloud Compute
[Click on image for larger view.] Figure 1: Standard Cloud Compute and Homomorphic Cloud Compute
The current approach to this problem scenario is for you to encrypt your data, then upload it to a cloud system. The data would have to be decrypted so that it can be processed. The result, which would be an ML prediction system or transformed data, would be encrypted on the cloud system, then transferred back to you where you would decrypt the results so they could be used.
There are two related problems with this approach. First, your data is not encrypted while it is being processed in the cloud. This creates a huge security vulnerability. Second, you must transfer the key to decrypt your data in the cloud. The cause of these problems is that data cannot be encrypted in order for it to be processed. This is where homomorphic encryption comes into play.
If your data could be processed while in encrypted form, then unencrypted data would never be outside of your immediate control. As shown on the right image in Figure 1, this would provide a much more secure computing environment.
Background and Development
The idea of creating encrypted data that could be operated on directly was explored at least as early as 1978. But it wasn't until 2009 that the first plausible algorithm was devised. In September 2009, university student Craig Gentry published "A Fully Homomorphic Encryption Scheme" as his dissertation paper. That algorithm worked in theory, but in practice it was far too slow to be useable. A single bit operation could take 30 minutes on the hardware of the time.
But research on homomorphic encryption immediately exploded. The term full homomorphic encryption means that any kind of computation -- addition, multiplication, comparison for equality, and so on -- can be performed on the encrypted data. Because of the extreme difficulty of the problem, researchers have looked at various sub-problems that are more tractable. Such a reduced system produces what is called partially homomorphic encryption. For example, the Levieil–Naccache scheme supports only the arithmetic addition operation, and the Goldwasser–Micali scheme supports only the exclusive-or bit operation. But the ultimate goal is a practical, fully homomorphic encryption system.
There are significant theoretical as well as practical problems related to homomorphic encryption. The main practical problem is performance. All current fully homomorphic system implementations are several orders of magnitude slower than operations on unencrypted data. One of several theoretical problems is called homomorphic malleability. This means that homomorphically encrypted data can be transformed into a different form of encrypted data. The differently-encrypted data cannot be decrypted, but it's still a valid encryption and is therefore a security risk.
Practical Applications
Many industry, academic, and government research labs are working on making practical homomorphic encryption a reality. Microsoft has created a C++ code library named SEAL (Simple Encrypted Arithmetic Library) that can do homomorphic encryption demos. Because using C++ is difficult, Microsoft also created a .NET code wrapper over SEAL so that engineers can easily experiment with homomorphic encryption. See the demo in Figure 2.
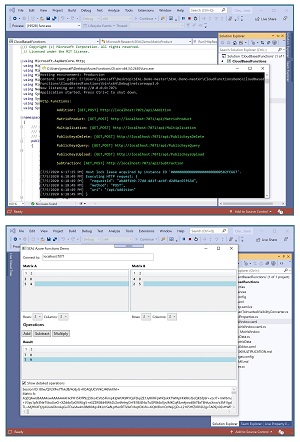 [Click on image for larger view.] Figure 2: Microsoft SEAL Library Demo
[Click on image for larger view.] Figure 2: Microsoft SEAL Library Demo
The SEAL demo has two components. The first component is a service that runs locally and simulates a cloud service. The second component is a GUI client. In the demo, the user inputs data for two, 2x2 matrices. The data is homomorphically encrypted and sent to the service. The service computes the matrix sum of the encrypted data and then sends the encrypted result back to the client. The client decrypts the result and displays it. The code is open source and fully available.
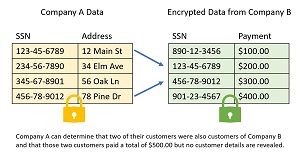 [Click on image for larger view.]Figure 3: Google Private Join and Compute Example
[Click on image for larger view.]Figure 3: Google Private Join and Compute Example
Google has created a C++ code library called Private Join and Compute (PJC). Although PJC can perform computation on homomorphically encrypted data, the target usage scenario is SQL-like data join operations. See Figure 3. Suppose a Company A has a database of customer information with Social Security Numbers as keys. Collaborating Company B has a database of payment information, also with SSNs as keys. The two companies wish to cooperate. Company B can homomorphically encrypt their data and send it to Company A. Company A can join the encrypted data and a limited aggregate sum can be computed, without revealing specific details of the data from Company B.
Looking Ahead
The Pure AI editors spoke to Dr. Kim Laine and Dr. James McCaffrey of Microsoft Research about the future of homomorphic encryption. Laine is a researcher in the Homomorphic Encryption Group. McCaffrey is a scientist engineer in the Deep Learning Group, and he was the author of the first publicly available .NET implementation of the Advanced Encryption Standard (AES).
McCaffrey commented, "Most of my colleagues suspect that progress on homomorphic encryption will move forward slowly and steadily until a threshold is reached."
McCaffrey added, "This possible evolution path is similar to the way machine learning gradually improved until a combination of enhanced algorithms, fast GPU computation, sophisticated code libraries, and big data technologies allowed deep neural networks to become truly practical and then ML exploded in usage."
Dr. Laine noted, "Two exciting new directions have showed up recently: automated optimization using techniques from programming languages and compilers, and hardware acceleration using GPU, FPGA, and possibly ASICs. And DARPA has recently launched a new project called DPRIVE with a goal of producing custom hardware for homomorphic encryption."
Both Laine and McCaffrey observed that the evolution of homomorphic encryption could also take a different path. "It's possible that a single breakthrough could revolutionize homomorphic encryption." They explained, "All current fully homomorphic schemes rely on the difficulty of mathematical lattice problems. Perhaps an algorithm based on factoring or discrete logarithms could lead to a huge jump in performance."