How-To
Researchers Explore Techniques to Reduce the Size of Deep Neural Networks
The goals are to save money (over $4 million for a single training run of a natural language model) and reduce CO2 emissions.
- By Pure AI Editors
- 06/02/2021
Deep neural networks can be huge. For example, the GPT-3 ("generative pre-trained transformer, version 3") natural language model has 175 billion trainable parameters. Huge neural networks can take days, months or longer to train, and this costs a lot of money -- reportedly over $4 million for a single training run of GPT-3. In addition to being expensive, the energy required to train a huge neural network produces a significant amount of CO2 emission.
Researchers have explored techniques for reducing the size of huge neural networks for decades. But these techniques are gaining increased attention as the size of deep neural networks, especially those designed for natural language processing and image recognition problems, steadily increase. Reducing the size of a neural network is sometimes called model compression but the term model pruning is most often used in research.
Understanding the Pruning Problem
Consider the simple 3-4-2 single-hidden layer neural network shown in Figure 1. There are three input nodes, four hidden layer processing nodes, and two output nodes. This architecture could correspond to a problem where the goal is to predict a person's gender (male, female) from their age, height, income. The network has (3 * 4) + (4 * 2) = 20 weights. Each weight is just a numeric value like -1.2345. Determining the values of a network's weights is called training the network.
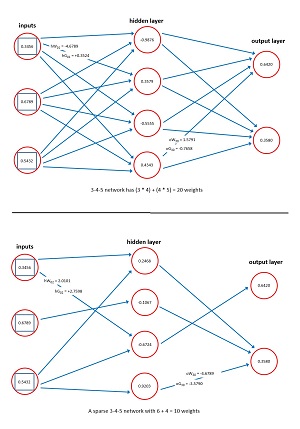 [Click on image for larger view.] Figure 1: Neural Network Weights, Gradients and Pruning
[Click on image for larger view.] Figure 1: Neural Network Weights, Gradients and Pruning
Note that in addition to ordinary weights, a neural network has a set of special weights called biases, one for each non-input node. The set of weights and biases are sometimes called the trainable parameters of the network. For simplicity, some research papers use the term weights to refer to both weights and biases.
A deep neural network is one that has multiple hidden layers. The number of input nodes and output nodes is determined by the problem data. But the number of hidden layers and the number of nodes in each hidden layer, are design choices ("hyperparameters") that must be determined by trial and error guided by experience. As the size of a deep neural network increases, the number of weights increases quadratically. For example, a natural language model might have to deal with approximately 40,000 vocabulary words. A relatively simple network with an architecture of 40000-(1000-1000-1000)-10 has (40000 * 1000) + (1000 * 1000) + (1000 * 1000) + (1000 * 10) = 42,100,000 weights.
Experience has shown that neural models that are over-parameterized are easier to train and produce more accurate prediction models than lean neural models. Loosely speaking, an over-parameterized model is one that is larger (and therefore has more parameters) than necessary. The goal of network pruning is to identify network weights that don't contribute much to the network output. Typically, these are weights that have small magnitudes. When pruned, for a given set of input values, the pruned network should produce nearly the same output values as the full non-pruned version of the network.
The Neural Network Lottery Hypothesis
The neural network lottery ticket hypothesis was proposed in a 2019 research paper titled "The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks" by J. Frankle and M. Carbin. Their summary of the idea is:
We find that a standard pruning technique naturally uncovers subnetworks whose initializations made them capable of training effectively. Based on these results, we articulate the "lottery ticket hypothesis:" dense, randomly-initialized, feed-forward networks contain subnetworks ("winning tickets") that -- when trained in isolation -- reach test accuracy comparable to the original network in a similar number of iterations. The winning tickets we find have won the initialization lottery: their connections have initial weights that make training particularly effective.
Put another way, it's possible to train a huge network, then prune away weights that don't contribute much, and still get a model that predicts well.
The lottery ticket idea has limited practical usefulness because it starts by training a gigantic neural network. Pruning occurs after training. This helps a bit at inference time when the trained model is used to make predictions, but running input through a trained model doesn't usually take much time so not much is gained. The lottery ticket idea is useful from a theoretical point of view -- knowing that huge neural networks can in fact be compressed without sacrificing very much prediction accuracy means that maybe it's possible to find a good compressed neural network before training rather than after training.
Single-Shot Network Pruning Before Training
A simple but promising network pruning technique was published in a 2019 research paper titled "SNIP: Single-Shot Network Pruning Based on Connection Sensitivity" by N. Lee, T. Ajanthan and P. Torr. The technique is based on neural network gradients. Neural networks are most often trained using variations of a technique called stochastic gradient descent (SGD).
During SGD training, each network weight has an associated value called a gradient. The value of a weight's gradient changes for each set of training inputs. The positive or negative sign of a gradient value tells the training algorithm whether to increase or decrease the value of the associated weight in order to produce network-computed output values that have smaller overall error. The magnitude of a gradient value tells the training algorithm how much to increase or decrease the value of the associated weight. Therefore, gradient values that have small magnitude, either positive or negative, will not result in much change to the associated weight.
The technique is simple. Before training, the network's weights are initialized to small random values using one of several mini-algorithms such as Glorot-uniform or Kaiming initialization. Then all training data is fed to the network and the gradients associated with each weight are computed. Then each gradient is normalized by dividing by the sum of the absolute values of the gradients. Network weights that have small normalized preliminary gradient values won't change much and so those weights are removed.
For example, suppose there are just eights weights in a fully connected neural network. On the preliminary pass, suppose the eight gradients are (1.2, -2.4, 0.8, 3.6, -1.8, 0.4, 2.8, 1.4). The sum of the absolute values is 1.2 + 2.4 + 0.8, + 3.6 + 1.8 + 0.4 + 2.8 + 1.4 = 14.4. The normalized gradients are (1.2/14.4, 2.4/14.4, . . . 1.4/14.4) = (0.08, 0.16, 0.06, 0.25, 0.13, 0.03, 0.19, 0.10). If the network pruning ratio is 50 percent, you'd drop the weights associated with the four smallest normalized gradients values: (0.03, 0.06, 0.08, 0.10).
Gradient Flow Preservation Pruning Before Training
A variation on the simple single-shot pruning technique was published in a 2020 research paper titled "Picking Winning Tickets Before Training by Preserving Gradient Flow" by C. Wang, G. Zhang and R. Grosse. The idea is to use second derivatives to estimate the effect of dropping a weight after pruning, rather than before pruning as in the simple single-shot technique. The motivation is the idea the gradient associated with a weight might change dramatically after pruning due to complicated interactions between weights.
The gradients used in stochastic gradient descent training are essentially estimates of the Calculus first derivative of the error function. It is possible to use Calculus second derivatives with a math technique called Taylor approximation to estimate the effect of removing a weight. Techniques that use Calculus second derivatives are called Hessian techniques.
Experimental results showed that the gradient flow preservation technique for pruning was clearly superior to random pruning before training, as expected. Additionally, for several image recognition problem scenarios, the gradient flow technique was able to prune a large network by 90 percent and achieve prediction accuracy nearly equal to that of the source over-parameterized network.
Wrapping Up
Dr. James McCaffrey works with deep learning engineering at Microsoft Research in Redmond, Wash. McCaffrey commented, "There's a general feeling among my colleagues that huge deep neural models have become so difficult to train that only organizations with large budgets can successfully explore them." He added, "Deep neural compression techniques that are effective and simple to implement will allow companies and academic institutions that don't have huge budgets and resources to work with state of the art neural architectures."
McCaffrey further noted, "Over the past three decades, there has been an ebb and flow as advances in hardware technologies, such as GPU processing, allow deep neural networks with larger sizes. I speculate that at some point in the future, quantum computing will become commonplace, and when that happens, the need for compressing huge neural networks will go away. But until quantum computing arrives, research on neural network compression will continue to be important."