How-To
Researchers Explore Differential Privacy
Differential privacy consists of a set of techniques designed to prevent the leakage of sensitive data.
- By Pure AI Editors
- 11/08/2021
The agenda of the recently completed 2021 International Conference on Machine Learning (ICML) listed over two dozen presentations related to the topic of differential privacy. What is differential privacy and what does it mean to you?
In a nutshell, differential privacy consists of a set of techniques designed to prevent the leakage of sensitive data. In most situations, when a dataset is queried, instead of returning an exact answer, a small amount of random noise is added to the query result. The query result is now an approximation, but an adversary cannot easily use the result to discover sensitive information.
The Netflix Example
One of the frequently cited examples related to the importance of data privacy is "Robust De-Anonymization of Large Sparse Datasets," A. Narayanan and V. Shmatikov, in Proceedings of the 2008 IEEE Symposium on Security and Privacy, May 2008. The paper examined a dataset of Netflix user movie reviews where personal information, such as user name, had been removed.
- When an adversary knows only a little bit of information about a particular record in the anonymized Netflix movie review dataset, the adversary can find the full record. Specifically, when an adversary knows just 8 movie ratings, of which 2 can be completely wrong, and dates that can have a 14-day error, 99 percent of records can be uniquely identified in the dataset.
- By using IMDB movie review dataset information, which does have personal information supplied by users, it is possible to match IMDB reviews with Netflix reviews and therefore find personal information that was removed from the Netflix dataset. This is called a linking attack.
Examples like this motivated interest in techniques to make data more private. Differential privacy is one such area of research and exploration.
Differential Privacy
Differential privacy (DP) is complicated and cannot be explained quickly. But loosely, one way to think about DP is that an algorithm is differentially private if you generate a data query result and can't use the result to determine information about a particular person. For example, suppose you have an artificially tiny dataset of just five items with sensitive age information:
ID Name Age
-----------------
001 Adams 40
002 Baker 30
003 Chang 50
004 Dunne 20
005 Eason 36
And suppose you can query the dataset for average age of two or more data items. If the average age of people 001 - 003 is 40.0 (therefore sum of ages is 120.0) and the average age of people 001 - 004 is 35.0 (therefore sum of ages is 140.0) then the age of person 004 is the difference of the sums = 140.0 - 120.0 = 20.0 years. Sensitive data has been leaked so this system is not differentially private.
The term "differential" in differential privacy is related to the idea of query results that differ by one item. Differentially private systems allow aggregate results, such as the average age of residents in a city from census data, to be made available without revealing specific information about an individual.
Adding Noise
The most common technique for making a system differentially private is to add random noise to a query result. For the average age query example, if the query asked for the average age of items 001 to 003, instead of returning the exact result of 40.0, a small random value, such as 2.5 is added to the result and 42.5 is returned.
The tricky part is determining how much random noise to add to a query result. More noise makes the system more private but makes the result less accurate. Much of differential privacy research is related to how to add random noise to query results to balance privacy and accuracy.
In most DP cases random noise is added using the Laplace distribution. You are probably familiar with the Gaussian (also called Normal, bell-shaped) distribution. The Laplace distribution is similar but instead of a rounded top, the Laplace has a pointy top. See Figure 1.
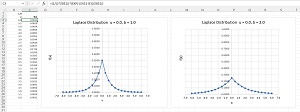 [Click on image for larger view.] Figure 1: The Laplace Distribution
[Click on image for larger view.] Figure 1: The Laplace Distribution
A Gaussian distribution has a mean (center value) and a standard deviation (measure of spread). A Laplace distribution has a "location" value (similar to a mean, and given symbol u) and a "scale" value (similar to a standard deviation, given symbol b). The x values can be between minus infinity and plus infinity. The area under a Laplace distribution probability density function sums to 1.0 and if you generate a random x value, you find the probability that x is between two values by computing the area under the curve.
Suppose the age query example adds random noise using a Laplace distribution with u = 0 and b = 1. The noise value will most likely be between -2.0 and +2.0 -- the query result will be close enough to the true average age to be useful, but cannot be easily used by an adversary to discover sensitive information about a specific data item.
Adding noise to queries that return numeric results is relatively easy. Adding noise to categorical results is much more difficult. Suppose you want to query a dataset for the country that a person lives in -- United States or Canada or Argentina and so on. Returning a random country is likely to not be very useful, so you must define a custom score for each county where a higher score is more accurate in some sense. Then for the query result, you select a semi-random county where countries with higher scores are more likely to be selected.
Differentially Private Data Clustering
Researchers are applying differential privacy techniques to standard machine learning techniques. One example is "Practical Differentially Private Clustering" posted on the Google research blog.
For data clustering, you group data items into k bins. Each bin has a representative value of some sort that represents all the data items in the cluster. Standard clustering algorithms, such as k-means or dbscan, are not differentially private. As a degenerate case, suppose an extreme value becomes its own k-means cluster of just one item -- you know everything about the item from the cluster mean.
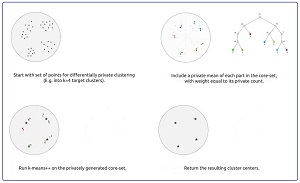 [Click on image for larger view.] Figure 2: Differentially Private Data Clustering (source: Google).
[Click on image for larger view.] Figure 2: Differentially Private Data Clustering (source: Google).
The differentially private clustering algorithm presented in the blog post first generates a coreset sample that consists of weighted items (with noise added) that represent the source data items well. The coreset is created using a technique called locality-sensitive hashing (LSH). This process is differentially private because it injects some randomness. After the coreset is created, any standard clustering algorithm can be applied. The result is clustering that is differentially private. Simple and elegant.
Note that like all differentially private algorithms, the clustering results are only approximations because of the random noise that is added. But that's the price you pay for differentially private algorithms.
Wrapping Up
Differential privacy is similar in some respects to cryptography in the sense that DP is paradoxically simple and complicated at the same time. In cryptography, to make a message secret all you have to do is scramble the message in some way. But scrambling a message so that an adversary cannot de-scramble it is astonishingly tricky. In the same way, to make a data query differentially private, all you have to do is add some random noise to the result. But the details and tradeoffs between query result accuracy and system privacy are quite tricky.