In-Depth
Machine Learning, Social Welfare and Fairness
With machine learning and economics becoming increasingly related, one area of active research concerns allocation, mathematical social welfare and mathematical fairness.
- By Pure AI Editors
- 10/05/2020
Machine learning and economics are becoming increasingly related. One area of active research concerns allocation, mathematical social welfare, and mathematical fairness. These ideas are best introduced using an example. Suppose three brothers, Adam, Brad, Carl, have inherited five items of jewelry (gold, jade, opal, ruby, teak) from an aunt. Each brother places a different subjective utility value, measured in utils, on each piece of jewelry according to the table in Figure 1. How should the five items be allocated to the three brothers?
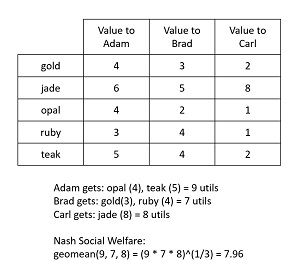 [Click on image for larger view.] Figure 1: Example of Nash Social Welfare
[Click on image for larger view.] Figure 1: Example of Nash Social Welfare
Using classical economics, a standard approach is to use Nash Social Welfare (NSW). The NSW principle says you should allocate items in a way that maximizes the geometric mean of the brothers' utility values. This solution is sometimes called maximum Nash welfare (MNW). For this problem, the NSW allocation is for Adam to get the opal (4) and teak items (5), Brad gets the gold (3) and ruby (4) items, and Carl gets the jade item (8). The utility values for each brother, assuming additive utility values, are 9, 7, 8. The geometric mean of (9, 7, 8) is the cube root of 9 * 7 * 8 = 7.96 utils.
There is no other allocation of jewelry items that would result in a larger geometric mean. Maximizing the geometric mean is equivalent to maximizing the product of each person's utility value. However, the geometric mean is used more often because it's a bit easier to interpret and compare against individual utility values.
Nash Social Welfare is named after John F. Nash, Jr. (1928-2015), an American mathematician who made fundamental contributions to several areas that are related to decision-making in complex systems. NSW is an extension of a technique published in Nash's 1950 paper "The Bargaining Problem" where just two people must allocate items.
All large companies have allocation problems, ranging from dividing a salary budget among employees, to assigning incoming network requests to servers. Some of the earliest recorded examples of allocation problems date back more than 2500 years. Allocation problems have received particular interest from companies that work at huge scale, such as Amazon, Facebook, and Google. Allocating many thousands or even millions of items is a very difficult problem.
Fairness and Envy
Allocation problems introduce the ideas of mathematical fairness and envy. There are many definitions of mathematical fairness. One definition which makes intuitive sense is that an allocation is fair if no person would prefer another person's set of items (bundle) to their own set of items. This definition of fairness is called envy-free (EF). For the jewelry example, Brad's set of items (gold 3, ruby 4) has the smallest value of 7 utils among the three brothers. Suppose Brad had Adam's items (opal, teak). Brad would value those items as opal = 2 and teak = 4 for a total of 6 utils, which is less than his current 7 utils. Or suppose Brad had Carl's item which is the jade. Brad would value the jade item as 5 utils, which is again less than his current 7 utils. In other words, one definition of allocation fairness is that no person would envy another person.
Notice that in the context of economics, the term social welfare refers to a narrowly focused idea of equity among agents rather than a more general idea related to ethics and moral values. In the same way, fairness refers to a mathematical definition of some sort rather than the more general meaning of impartiality and justice.
Envy-free allocation is a strict criterion. In research, a common idea is to find an allocation that has some upper bound of envy. For example, "envy-free except one" (EF1) means for every pair of persons A and B, there is one item in B's bundle that can be removed, and then A will not envy B. So, stated loosely, an EF1 allocation is not quite as strict as an EF allocation.
In addition to the notion of mathematical fairness, an allocation algorithm can be analyzed to see if it has various nice mathematical properties or not. Some of these properties include Pareto-optimality, symmetry, scale-invariance, irrelevant-independence, and resource-monotonicity. In spite of its simplicity, NSW satisfies all these attributes except resource-monotonicity. The 2016 paper, "The Unreasonable Fairness of Maximum Nash Welfare", by I. Caragiannis, et al. provides a rigorous math explanation.
Machine Learning and Allocation
For allocation problems and fairness, machine learning enters the picture in two ways. First, computing an exact NSW or similar allocation is very difficult and so machine learning techniques have been used to find approximate solutions. Second, for machine learning algorithms that explicitly or implicitly generate an allocation, you can analyze allocation results for mathematical fairness.
The jewelry allocation problem is an example where the items are not divisible. Each brother must get an item or not. It's not possible to take the jade item and give 0.60 of it to Adam, 0.10 of it to Brad, and 0.30 of it to Carl. This makes allocation with non-divisible items a combinatorial optimization problem where the challenge is to partition n items among k people. Combinatorial optimization problems are among the most difficult in machine learning, in part because of the combinatorial explosion issue.
The number of ways to partition n items into k subsets is called a Stirling number of the second kind, often written as S(n, k). For example, S(4, 2) is the number of ways to group 4 items into 2 subsets and is 7. Suppose the four items are a, b, c, d. The seven partitions are: (a | bcd), (b | acd), (c | abd), (d | abc), (ab |cd), (ac | bd), and (ad | bc).
For the jewelry example, S(5, 3) = 25 and so to compute the NSW allocation you could use brute force to examine each possible allocation and select the one that has the largest geometric mean of utility values. However, the value of S(n, k) gets astronomically large, very quickly. For example, S(100, 3) = 85,896,253,455,335,221,205,584,888,180,155,511,368,666,317,646.
 [Click on image for larger view.] Figure 2: Computing the Number of Ways to Allocate n=100 Items to k=3 Groups
[Click on image for larger view.] Figure 2: Computing the Number of Ways to Allocate n=100 Items to k=3 Groups
In general, it's not possible to examine every possible allocation of non-divisible items. Because of this characteristic, there are several ways to find an approximate NSW solution. These include techniques used in machine learning such as epsilon-greedy agglomeration, and evolutionary combinatorial optimization.
In epsilon-greedy agglomeration, you start with each person/agent having one randomly selected item. Then you iterate through each person, adding the item that most increases the geometric mean of the utility values, or with small probability epsilon you add a randomly selected item. For example, see the 2018 paper "Greedy Algorithms for Maximizing Nash Social Welfare" by S. Barman, et al.
In evolutionary combinatorial optimization, you create a population of many allocations. From these, you select a few of the good allocations and then mutate each good allocation by switching the assignments of two items and other rearrangements. You repeat this process until you are satisfied.
In many practical allocation problems, items are not divisible. But if items are divisible, then classical numerical convex optimization techniques can be used to find a Nash Social Welfare solution. For problems with non-divisible items, in addition to the epsilon-greedy and evolutionary approaches, another way to approximate a solution is to assume items are divisible, get that exact solution, and then convert partial items (such as 0.40 of the gold item) to whole items. See the 2015 paper "Approximating the Nash Social Welfare with Indivisible Items" by R. Cole and V. Gkatzels.
There are many areas of research that are related to pure allocation. One example is bidding for online advertising resources. The 2020 paper "Robust Market Equilibria with Uncertain Preferences" by Riley Murray et al. explored online advertising where items are scare and divisible, and buyers compete for items. The fundamental model in such scenarios is called a linear Fisher market. The model is named after Irving Fisher (1867-1947), an American economist. The paper looked at scenarios where there is uncertainty in valuations which makes the problem scenario very difficult.
Comments from the Experts
The Pure AI editors contacted Dr. Michael Schwarz, Microsoft Corporate Vice President and Chief Economist, and talked with him about the connection between machine learning and economics. Schwarz described projects that used deep neural technologies. He commented, "Making more intelligent forecasts and using these forecasts more intelligently made it possible to better allocate hardware among datacenters and better allocate investments among hardware types, thus simultaneously lowering total hardware costs and reducing probability of hardware shortages."
Riley Murray, a doctoral candidate at Cal Tech and lead author of the Robust Equilibria paper, offered the opinion, "The application of ML in economics will take a while to see widespread adoption." Murray added, "Traditionally economists build models not for their predictive power, but to infer structural properties induced by a mathematical model (e.g. a notion of fairness)."
The Pure AI editors also spoke to Dr. James McCaffrey, a machine learning engineering expert from Microsoft Research. McCaffrey noted, "I suspect that the use of neural-based machine learning in economics will increase steadily, mostly in specialized problem scenarios where the goal is a predictive model, such as in hedge funds and complex time series regression."