How-To
Understanding Variational Autoencoders – for Mere Mortals
Here's an explanation of variational autoencoders -- one of the fundamental types of deep neural networks -- used for synthetic data generation.
- By Pure AI Editors
- 05/18/2020
Variational autoencoders are one of the fundamental types of deep neural networks. Autoencoders are another important type of deep neural network. Deep neural autoencoders and deep neural variational autoencoders share similarities in architectures but are used for different purposes.
Autoencoders and MNIST Data
Autoencoders usually work with either numerical data or image data. Three common uses of autoencoders are data visualization via dimensionality reduction, data denoising, and data anomaly detection. Variational autoencoders usually work with either image data or text (document) data. The most common use of variational autoencoders is for generating new image or text data.
The best way to understand autoencoders (AEs) and variational autoencoders (VAEs) is to examine how they work using a concrete example with simple images. The most common example data for understanding AEs and VAEs is the MNIST image dataset. The MNIST dataset consists of 70,000 images. Each image is a 28 pixel by 28 pixel (784 total pixels) picture of a handwritten digit ("0" through "9"). Each pixel in an image is represented as a grayscale value from 0 to 255. The MNIST dataset is divided into 60,000 images designated for training a neural network, and 10,000 images designated for testing.
 [Click on image for larger view.] Figure 1: Examples of MNIST Digits
[Click on image for larger view.] Figure 1: Examples of MNIST Digits
The images in Figure 1 show examples of MNIST digits. On the left is a "5" digit displayed in an Excel spreadsheet. Each cell of the spreadsheet represents one pixel and holds a value between 0 and 255. The cells are formatted so that larger pixel values are darker. On the right are six other MNIST digits that were displayed using a Python language program.
A deep neural AE is trained by having the AE predict its own input. The architecture of an AE for MNIST has 784 input nodes, and 784 output nodes, one for each pixel. The autoencoder at the top of Figure 2 uses just five input/output nodes to illustrate the idea and keep the size of the diagram reasonable.
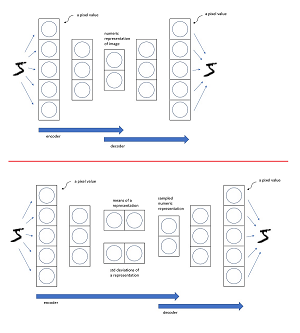 [Click on image for larger view.] Figure 2: Architectures of an Autoencoder (top) and a Variational Autoencoder (bottom)
[Click on image for larger view.] Figure 2: Architectures of an Autoencoder (top) and a Variational Autoencoder (bottom)
At the core of the example AE is a vector with two values between 0.0 and 1.0. These two values, along with the weights of the AE which are not shown, are a condensed numeric representation of an input image. For example, 784 pixel values which are all between 0 and 255 each, might be represented as (0.5932, 0.1067). These two core values can be used to create a visualization of the image because you can plot two values on an x-y graph. Put another way, the AE has been used to reduce the dimensionality of an MNIST image from 784 to 2.
When used for dimensionality reduction the decoder part of the AE architecture, which was needed for training, is not used. The size of the core representation is 2 in this example, but could be any size.
A second way to use an AE is to smooth a dataset, sometimes called denoising. You feed image data into the AE and capture the output data. The output data will be very close to, but not exactly the same as, the original data. The compression-inflation mechanism of the AE removes unusual characteristics of the data. When used in this way, both the encoder and decoder parts of the AE are used.
A third, related way to use an AE is to feed images into the AE and compare how well the 784 output pixel values match the 784 input values. Images which have a large difference, the reconstruction error, are somehow different from the majority of data items and are likely to be anomalies.
To summarize, an autoencoder predicts its own input. The core representation of a data item in an AE has a lower dimension than the source data. If an autoencoder core representation has size 2, it can be used to create a graph of the source data. Autoencoders can also be used to denoise data, or to identify anomalous data by looking at the reconstruction error.
Variational Autoencoders
The motivation for VAEs is the problem of generating synthetic data that is based on existing data. For the MNIST data you would want to create artificial 28 × 28 images that look as though they are actual images from the dataset. If you used a regular AE for synthetic image generation, you would take two random values such as (0.9016, 0.5427) and feed them to the decoder part of the AE. The output result would be 784 pixel values. However, if you displayed these pixel values, the result wouldn't look much like a digit.
The problem is that during training, an AE tries its best to find two values that represent a particular digit image as closely as possible. Suppose a "5" image is represented in an AE as (0.1234, 0.5678). If you feed two values that are close, such as (0.1239, 0.5670), to the decoder of the AE, you will likely get pixel values that look very much like a "5" digit. But there is little relationship between the representational values of different digit images. So, when you feed an AE two values that don't closely match those generated by the training data, the result is likely to not resemble any of the source data used to train the AE.
A deep neural VAE is quite similar in architecture to a regular AE. The main difference is that the core of a VAE has a layer of data means and standard deviations. These means and standard deviations are used to generate the core representations values. For example, during training, a "5" image might have means of (2.0, -1.0) and standard deviations of (0.80, 0.50). The two core representation values of the VAE are generated probabilistically. For example, the first core representation could be 2.0 + 0.40 = 2.40 and the second core representation value could be something like -1.0 + 0.25 = 0.75 and so the core representation is (2.40, 0.75). The means and standard deviations of a VAE are usually based on a Gaussian bell-shaped distribution.
The reason why this VAE scheme helps for generating synthetic images isn't obvious. The means and standard deviations to representational values adds a variability that is missing from standard AEs. For example, in a VAE if a "5" digit has a core representation of (0.1234, 0.5678) the representation was generated from many values rather than a few values. Therefore if you send to a VAE values that are only just somewhat close to (0.1234, 0.5678), such as (0.1200, 0.5500), the result will likely resemble a "5" digit.
Another way of thinking about why the means and standard deviations to core representation values is beneficial for generating data is that the variability component of VAE architecture acts to cover the entire range of possible input values to the decoder. Put another way, a regular AE has huge gaps in possible input values to the decoder, but a VAE has fewer input value gaps.
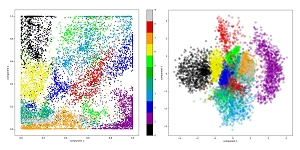 [Click on image for larger view.] Figure 3: MNIST Digits by Autoencoder (left) and Variational Autoencoder (right)
[Click on image for larger view.] Figure 3: MNIST Digits by Autoencoder (left) and Variational Autoencoder (right)
The graphs in Figure 3 illustrate why VAEs work better than AEs for generating synthetic data. Each graph shows the same set of 10,000 MNIST images. The AE shown on the left represents each MNIST digit image, which the AE made as distinct as possible from each other. This leads to gaps between data points. The x and y coordinates are the core representation values. This is good for classification but bad for data generation. For example, if you fed input values of (0.9, 0.4) to the AE, you're at an unknown white area between the purple "1" images and the dark blue "2" images, and so the resulting synthetic image would appear as random pixel values.
The VAE on the right plots the two core mean values on the graph x-y axes. Each mean-pair can generate many representations, suggested by the wider diameter of the display dot. Additionally, VAE architecture encourages image representations to be close to each other, greatly reducing the unknown area gaps between data points.
 [Click on image for larger view.] Figure 4: Synthetic Images Generated by Variational Autoencoder
[Click on image for larger view.] Figure 4: Synthetic Images Generated by Variational Autoencoder
Figure 4 shows 100 synthetic images generated by a VAE with core representation of two values. One hundred pairs of values were fed to the decoder part of the VAE and the output 784 pixels were graphed. You can see that most of the synthetic images look as though they could have come from the real MNIST dataset. For example, the input of (0.4, 0.4) generated a very realistic "6" image.
Wrapping Up
Variational autoencoders were originally designed to generate simple synthetic images. Since their introduction, VAEs have been shown to work quite well with images that are more complex than simple 28 x 28 MNIST images. For example, it is possible to use a VAE to generate very realistic looking images of people. VAEs can also be used to generate synthetic text documents that read as though they were written by a real person, and VAEs can generate synthetic music.
Variational autoencoders are just one form of deep neural network that are designed to generate synthetic data. Other generative deep neural architectures include GANs (Generative Adversarial Networks), usually used for image generation, and BERT (Bidirectional Encoder Representations from Transformers), for natural language processing.
A question that's not so easy to answer is, "Why is there so much research effort aimed at generative models?" The usual explanation from researchers is that understanding how deep neural systems can generate synthetic data may give insights into cognition -- how humans acquire and learn knowledge. This would be a giant step forward towards the goal of creating general AI systems.
Other questions related to the ability to generate realistic synthetic data concern security. Dr. James McCaffrey, from Microsoft Research, commented, "There's no question that the ability to create realistic synthetic data using deep generative models such as VAEs raises serious security issues. I suspect that these sophisticated generative systems will increase the importance of ways to verify the provenance and authenticity of digital artifacts."