How-To
Researchers Explore Quantum-Inspired Optimization
- By Pure AI Editors
- 12/01/2021
Machine learning researchers are actively exploring quantum-inspired optimization. Quantum-inspired optimization starts with a standard algorithm, such as particle swarm optimization or simulated annealing, and modifies the algorithm by using one of many ideas adapted from physics quantum behavior. Quantum-inspired optimization (QIO) is not the same as quantum computing (QC). QIO uses standard hardware and software, as opposed to QC which uses exotic hardware and highly specialized software.
Quantum-Inspired Annealing
The idea of quantum-inspired optimization is best explained by a concrete example. Figure 1 shows standard simulated annealing and quantum-inspired annealing being used to solve a combinatorial optimization problem. The goal of a combinatorial optimization problem is to find the best ordering of a set of discrete items. The most well-known example of a combinatorial optimization problem is the Traveling Salesman Problem. In TSP, the goal is to find the best order in which to visit a set of cities, so that the total distance traveled is minimized.
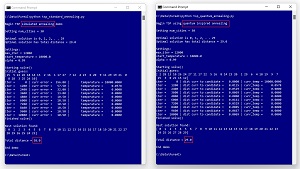 [Click on image for larger view.] Figure 1: Standard and Quantum-Inspired Annealing for Traveling Salesman Problem
[Click on image for larger view.] Figure 1: Standard and Quantum-Inspired Annealing for Traveling Salesman Problem
Standard simulated annealing loosely mimics the behavior of cooling metal. Expressed in high level pseudo-code, standard simulated annealing is:
create an initial random guess solution
set large starting temperature
loop many times
create an adjacent candidate solution
if candidate is better than current then
replace the current solution with candidate
else-if candidate is worse
replace current anyway with probability
based on current temperature
end-if
reduce temperature slightly
end-loop
return best solution found
With regards to quantum-inspired optimization, the relevant part of simulated annealing is the creation of an adjacent candidate solution. For example, suppose that for a five-city TSP scenario, a current solution is [3, 0, 4, 2, 1]. An adjacent candidate solution is one where two randomly selected cities have been swapped. If the two randomly selected indices are [0] and [2], then the adjacent candidate solution is [4, 0, 3, 2, 1].
The idea of using an adjacent candidate solution is that the candidate will be similar to the current solution and therefore a good current solution will likely generate a good adjacent solution. However, one problem with this approach is that it's difficult to explore a wide range of possible solutions. Note that looking at every possible permutation isn't feasible. For 30 items, there are 30! = 30 * 29 * 28 * . . * 1 = 265,252,859,812,191,058,636,308,480,000,000 possible permutations. Even if you could evaluate one million permutations per second, examining all permutations would take 8,411,113,000,000,000,000 years -- much longer than the estimated age of the universe (13,800,000,000 years).
Quantum-inspired annealing incorporates the idea of quantum particle tunneling. Briefly, a quantum particle will usually transition to an adjacent state. But sometimes a quantum particle will jump to a non-adjacent state. Motivated by this phenomenon, one possible realization of quantum-inspired annealing is:
create an initial random guess solution
set large starting temperature
set current time
loop many times
with small probability based on current time
create a tunneling non-adjacent candidate
else
create an adjacent candidate solution
if candidate is better than current then
replace the current solution with candidate
else-if candidate is worse
replace current anyway with probability
based on current temperature
end-if
reduce temperature slightly
end-loop
return best solution found
All forms of annealing optimization are metaheuristics, meaning a set of general guidelines rather than a rigid prescription. Therefore, there are many possible concrete implementations. Similarly, there are many quantum behaviors that could inspire modifications to standard optimization techniques. For example, a quantum packet is a collection of quantum particles. This could motivate an annealing algorithm that uses multiple possible solutions, possibly being manipulated by different physical CPU or GPU processors. In short, the goal of quantum-inspired optimization is a better optimization algorithm, not a high-fidelity simulation of quantum behaviors.
Quantum-Inspired Particle Swarm Optimization
Quantum-inspired optimization can be used for problems other than combinatorial optimization. Standard particle swarm optimization (PSO) is used to solve problems where the goal is to find the best solution which has the form of a numeric vector (set of numeric values). An example is finding the best settings for a complex environmental control system.
A PSO algorithm uses a set of possible solutions called particles. On each iteration of the algorithm, every particle "moves" to a new position (candidate solution). The new position is a weighted combination of the best position seen so far by the particle and the best position seen by any particle in the swarm. For example, suppose a particle's current position is (3.0, 7.0, 2.0), and the best position seen by the particle was at (5.0, 8.0, 4.0), and the best position seen by any particle was (6.0, 9.0, 3.0). The particle might move to a new position close to (5.5, 8.5, 3.5).
The diagram in Figure 2 shows a hypothetical example of the first four iterations of a problem where a solution / position has two numeric elements (x0, x1) and the swarm consists of just two particles (blue and green). On each iteration the two particles move closer to the red dot optimal solution at (0, 0). The spiral motion is characteristic of PSO.
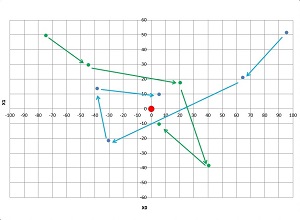 [Click on image for larger view.] Figure 2: Particle Swarm Optimization
[Click on image for larger view.] Figure 2: Particle Swarm Optimization
The math equations that control the movement of particle-solutions in the swarm are based on empirical experimentation rather than physics. Quantum-inspired PSO adapts the motion equations in a way that's inspired by quantum behavior.
In the paper "Three Novel Quantum-Inspired Swarm Optimization Algorithms using Different Bounded Potential Fields" (M.S. Alvarez-Alvarado, et al., Nature Scientific Reports, June 2021), three different quantum behaviors were applied to standard PSO. The three quantum behaviors were Lorentz, Rosen-Morse, and Coulomb-like square root potential fields. The researchers found that the algorithm inspired by Lorentz potential field behavior presented the most balanced performance in terms of exploitation (accuracy and precision), exploration (convergence speed and acceleration), and simulation time.
What Does It All Mean?
Dr. James McCaffrey from Microsoft Research works with combinatorial optimization and swarm optimization. McCaffrey commented, "Quantum-inspired optimization techniques have the potential to make a big impact in several fields." He added, "Some of my colleagues and I believe that when more compute processing power becomes available, quantum-inspired optimization may provide significant breakthroughs for training deep neural networks with billions or trillions of weights."
Solving complex combinatorial and numerical problems in practice involves more than standard or quantum-inspired algorithms. Dr. Pawel Lichocki works on combinatorial optimization at Google. He observed, "When applying combinatorial optimization to real life problems, half of the time spent is in the discovery phase." Lichocki added, "The other half is implementation, and half of that is getting the data. I would say ten percent of your work is on coding."